Viết về một người sắp ra đi, Toàn Phong Nguyễn Xuân Vinh

Theo tin từ BS Nguyễn Thượng Vũ ngày 11 tháng 07, 2022 cho biết là sức khỏe của GS Toàn Phong Nguyễn Xuân Vinh đã suy sụp rất nhiều. Bệnh viện đồng ý là với tình trạng sức khỏe của GS Vinh, ở tuổi 92 của GS Vinh thì không thể nào có hy vọng hồi phục được. Bác sĩ điều trị sẽ áp dụng Hospice Care cho anh GS Vinh. (Hospice Care có nghĩa là bác sĩ điều trị sẽ dùng mọi phương tiện để GS Toàn Phong Nguyễn Xuân Vinh sẽ thoải mái, không bị đau đớn trong thời gian sắp tới).
Sáng nay khi tôi (Việt Hải) đuợc tin về GS. Nguyễn Xuân Vinh đã vào tình trạng hospice care unit, tôi buồn lắm. Tôi còn nhớ khi ông dọn từ San Jose về Huntington Beach (Orange County), 12 anh chị em nhóm chúng tôi đến thăm thầy, lý do riêng GS. Phạm Hồng Thái bàn về sách Thiên Chức Của Nhà Giáo với GS. Vinh sẽ khởi sự: Nguyen X Vinh (Vietnamese Edition) Paperback – June 20, 2018, do NXB Amazon. Vietnamese Edition by Nhân Văn Nghệ Thuật (Author), GS Đào Đức Nhuận (Editor), GS Phạm Hồng Thái (Editor, Designer).

Những năm khi NASA thám hiểm cung trăng, Apollo 11 là chuyến bay không gian đã hạ cánh cùng người đầu tiên đáp xuống Mặt Trăng, hai phi hành gia Hoa Kỳ là Neil Armstrong và Buzz Aldrin, vào ngày 20 tháng 7, năm 1969, lúc 20:18 UTC. Armstrong trở thành người đầu tiên bước chân lên bề mặt của Mặt Trăng sáu giờ sau vào ngày 21 tháng 7, lúc 02:56 UTC. Armstrong dành hai tiếng rưỡi bên ngoài con tàu không gian, trong khi Aldrin có ít thời gian hơn một chút và cùng nhau, họ thu thập 47.5 pounds (21.5 kg) Đá Mặt Trăng cho chuyến trở về Trái Đất. Thành viên thứ ba của Phi hành đoàn, Michael Collins, lái Module (space lab unit) Điều Khiển một mình quanh quỹ đạo của Mặt Trăng cho đến khi Armstrong và Aldrin quay về Module Điều Khiển chỉ một ngày trước khi họ phải bắt đầu hành trình quay về Trái Đất. Vê sau KHG David Scott chỉ huy tàu Apollo 15 đáp xuống Mặt trăng vào tháng 7, 1971. Trong chuyến thám hiểm này, ông cùng cộng sự đã điều khiển 3 chiếc xe điện chuyên dụng để thu thập các mẫu đất đá và mang về nghiên cứu. James Irwin bên cạnh lá quốc kỳ Mỹ trong chuyến thám hiểm Mặt trăng.
Những năm này thế giới khoa học gia không gian chú ý đến GS. Nguyễn Xuân Vinh, người đã lead team dùng toán học tính quỹ đạo bay ra ngoài không gian và về trái đất (During this expedition, he and his colleagues drove 3 specialized electric vehicles to collect soil and rock samples and bring them back for research. James Irwin next to the American flag during his exploration of the Moon. In these years, the world of space scientists paid attention to Prof. Nguyen Xuan Vinh, who led the team to apply math to calculate the orbiter flight path by space vehicles, fly to space and back to earth).
Tôi viết về thầy Vinh: “Tưởng cũng nên ghi nhận tác giả là một vị giáo sư toán giảng dạy bậc cấp cao (advanced mathematics), và cũng là một khoa học gia ngành không gian, mà đề tủ của ông là Optimal Trajectories, ông viết sách về Quỹ Đạo Tối Ưu, sách toán hay không gian học của Mỹ, Pháp, Nga, Nhật,… đều có đăng những bài do ông viết. Do vậy tác giả Nguyễn Xuân Vinh là người của thế giới, họ biết ông qua những kiến thức chuyên môn của ông, mà toán học và không gian học là hai yếu tố then chốt tạo nên tên tuổi của tác giả. Nói như vậy không có nghĩa là Vui Đời Toán Học được ươm mầm bởi những lý thuyết toán học cao siêu của những Joseph Lagrange, Laplace, Euler, Fourier, Boole, Cauchy, Leibniz, Isaac Newton, Jacob Bernoulli, Johann Bernoulli, Bourbaki, Neumann, Niels Abel, Plato, Blaise Pascal, Pythagore, René Descartes,… “.
GS. Vinh đi bên toán học, không gian học và văn học thì đã có nhiều nhiều campus fans vốn hâm mộ. Khi làm về ngành R&D, Weapon Innovation Development, tính đường bay của phi đạn, tôi quý môn toán học (missile systems flight path). GS. Vinh là một sharp scientist như những Johannes Kepler hay Katherine Johnson, Dr. Katherine Johnson đã góp công lớn cho những thành tựu về toán học, nhà toán học Mỹ, tính toán và phân tích đường bay của nhiều con tàu vũ trụ.
Toàn Phong Nguyễn Xuân Vinh, Một Tấm Gương Kiên Nhẫn Cho Giới Trẻ, bài viết của ông Nguyễn Tường Tâm, 4/10/2005

Trong môt bài viết bằng tiếng Anh để gửi tới giới trẻ trong buổi hoàng hôn của cuộc đời mình, nhà văn, nhà khoa học và cũng là một vị cựu Tư Lệnh Không Quân VNCH, Toàn Phong Nguyễn Xuân Vinh đã tâm sự:
Our journey across life can be compared to the flight of an aircraft across a vast ocean. Sometimes we are favored by a tail wind which gives us a faster ground speed. But sometimes on other occasions, we may face a head wind with adverse effects. As the first generation of immigrants, we are the pioneers, and we may run into obstacles. Just as the aircraft has to get to the other side of the ocean because it has passed the point of no return, when facing the head wind in our life, such as in the case of social injustice, we should keep our heads high, our chins up, and then with physical endurance, technical expertise, and with spiritual strength, by dedication and dignity, we shall join force together to overcome adversity and fulfill our dream of equal opportunity, equal rights and equal responsibility, and in so doing, make it a reality.
Đoạn văn có ý khuyên người đọc rằng trong cuộc đời nếu muốn thực hiện một điều gì cho riêng mình hay cùng nhau chiến đấu cho một lý tưởng quốc gia mà gặp khó khăn trở ngại thì cứ nên giữ vững lòng tin vào chính nghĩa, để với quyết tâm và tự trọng và cùng nhau liên kết thì cũng như một chiếc phi cơ phải bay qua đại dương, sẽ có lúc sang được phía bờ bên kia. Câu viết này có thể dùng cho những đoạn đời đã qua của giáo sư Nguyễn Xuân Vinh. Con người ông đã là một kết hợp của một loạt những ước mơ thường là tương phản nhau mà ông đã hoá giải được để cùng thực hiện. Ông mơ những giấc mơ mâu thuẫn nhau và ông thường làm ngược với những người cùng hoàn cảnh. Nhưng cuối cùng ông đã thực hiện được tất cả những ước mơ tưởng chừng như không thể nào kết hợp được trong cùng một con người và trong thời gian hạn hẹp của đời người .
Trước tiên, thấm nhuần nho học gia đình nhưng chàng tuổi trẻ Nguyễn Xuân Vinh lại ham mê tây học và khoa học và có ước mơ canh tân đất nước. Trong một xã hội Việt nam thời đó, khi mà người ta thường nói “phi cao đẳng bất thành phu phụ!” nghĩa là nếu không có bằng Bác sĩ , Luật sư thì không được người đời qúy trọng, tuy ông có khả năng để đạt được những mảnh bằng đó một cách dễ dàng, mà ông lại không theo con đường chung của mọi người. Ông chọn môn Toán học mà ông mê thích và đi theo con đường này thì vừa khó khăn gấp bội mà lại chẳng có danh, cũng không có lợi. Người sinh viên theo ngành này, nếu không phát minh được một lý thuyết nào và đạt được trình độ tiến sĩ thì sẽ chỉ trở thành một ông giáo bình thường mà thôi . Ông mê học toán tới độ khi kháng chiến bùng nổ, ông theo gia đình tản cư nhưng vẫn tiếp tục học để lấy chứng chỉ Toán đại cương trong hoàn cảnh thiếu thầy, thiếu lớp và thiếu cả sách vở. Giữa năm 1950, vừa theo gia đình hồi cư về Hà Nội, ông tiếp tục ghi tên theo học ngay hai trường đại học dược khoa và đại học khoa học để học lại lần thứ nhì lớp Toán đại cương mà ông chưa hoàn tất ở khu kháng chiến. Tại đại học Hà Nội, ngoài giờ trong lớp ông còn làm phụ tá cho giáo sư để lấy tiền theo đuổi việc học. Và ông đã đỗ đầu kỳ thi chứng chỉ Toán đại cương vào đầu hè năm 1951 và được tuyển làm giáo sư trường Trung học Nguyễn Trãi Hà Nội .
Năm 1951, bất ngờ ông nhận được giấy gọi nhập ngũ theo học khoá I Sĩ quan Trừ bị Nam Định và được chuyển theo học chuyên môn về công binh ở Thủ Đức. Ông là một trong số chỉ chừng vài chục người có thể tự nhận rằng đã được theo học tại cả hai quân trường Võ khoa Nam Định và Võ khoa Thủ Đức. Ra trường ông là một sĩ quan công binh và nơi đồn trú đầu tiên của ông là tỉnh Thái Bình .
Khoảng thời gian này, một lần nữa ông lại phải lấy một trong hai chọn lưạ mâu thuẫn nhau. Là một người ham học, đáng lẽ ông có thể vừa ở nhiệm sở vừa ghi tên theo học toán tại Đại học Hà Nội, nhưng vì ôm mộng hải hồ nên trước khi đi nhận nhiệm sở sĩ quan công binh, ông đã nạp đơn dự thi vào trường Không Quân Pháp. Vào thời điểm đó, Không Quân Việt Nam chưa được thành lập. Một đại uý không quân được cử từ Pháp sang Saigon để phát bài thi cho thí sinh đồng thời ông ta cũng sẽ là giám khảo phần thi vấn đáp. Có chừng 20 người dự thi . Nhưng có lẽ bài thi viết cuả ông quá xuất sắc nên vị sĩ quan giám khảo thay vì khảo hạch ông trước bảng đen cuả lớp học thì lại mời ông ra đứng ở lan can phòng thi kể cho ông nghe viễn tượng đang chờ đợi ông ở quân trường không quân ở miền Nam nước Pháp . Nghe thấy vậy ông đã tin gần chắc là ông sẽ đỗ. Quả nhiên mấy ngày sau, trong số 5 thí sinh trúng tuyển, ông đã được chọn đỗ đầu, trong khi lúc chính thức vào phòng vấn đáp ông không phải nói một câu nào ngoài câu chào lúc bắt đầu và câu cám ơn lúc kết thúc .
Sau mấy tháng làm sĩ quan công binh tại Thái Bình ông nhận được giấy vào Saigon đi học trường không quân Ecole de l’Air cuả Pháp nằm ở tỉnh Salon de Provence. Trước đó điều kiện để được nhập học trường này rất khó, vì phải vừa là dân Tây vừa phải theo học một lớp toán học cao cấp sau tú tài 2. Cho nên trước đó mới chỉ có 2 người Việt quốc tịch Pháp được theo học, trong đó có trung tướng Nguyễn văn Hinh. Trước ông 2 năm cũng có một sĩ quan người Việt là ông Lê Trung Trực, sau này là chuẩn tướng không quân, được nhận như là một sinh viên ngoại quốc. Như vậy ông Nguyễn Xuân Vinh là một trong 5 khóa sinh Việt nam đầu tiên học trường này qua một kỳ thi tuyển lựa như thí sinh Pháp và cũng là một trong 3 người Việt nam đầu tiên được trúng tuyển theo học ngành phi hành với 2 người nữa theo học ngành kỹ thuật.
Sang Pháp , trước tiên ông được gửi tới trường phi hành (École de pilotage) ở Marrakech. Sau chín tháng được huấn luyện bay ông nhận được giấy tới Salon de Provence để nhập học Khoá sĩ quan không quân 1953. Tại thời điểm này, Nguyễn Xuân Vinh lại kết hợp 2 con người mâu thuẫn trong ông, một con người quân sự, vẫy vùng, ngang tàng, và con người sinh viên chăm chỉ nơi giảng đường đại học. Trước ngày khai trường, được nghỉ hai tháng hè, lợi dụng thời gian này ông tới Nice để học thi chứng chỉ Toán Vi Phân và Tích Phân mà ông đã ghi tên học từ đầu năm ở Đại Học Marseille. Ông đã từng viết lên tâm sự rằng, trong khoảng thời gian những năm cuối cùng sống trên đất Pháp, ông cố thu thập những lý thuyết quân sự, tổ chức hành chánh, kỹ thuật và hành quân trong Không Quân, và đồng thời cũng nhân dịp còn ở nước người, học thêm về toán học, về những môn chưa được giảng dậy tại quê nhà để sau này có dịp đưa kiến thức và sở học ra phục vụ quê hương một cách đắc lực hơn. Với suy nghĩ như vậy cho nên , sau đó, cùng với việc tốt nghiệp một trường sĩ quan phi công nổi tiếng cuả Pháp, ông cũng đã lấy được bằng cao học Toán tại đại học Marseille. Trong một lần tâm sự, tôi có hỏi ông rằng, trong thời gian học phi công quân sự tại Pháp, nhất là tại kinh thành Ánh Sáng, cuối tuần các sinh viên sĩ quan thường đưa đào đi chơi, uống rượu, nhẩy đầm, thì làm sao GS lấy được bằng cử nhân rồi cao học toán . Ông nhìn tôi bằng đôi mắt to và lúc nào trông cũng có vẻ hiền lành, thản nhiên cho biết: “cuối tuần, trong lúc các sinh viên sĩ quan khác đi chơi thì tôi đi học .” Thật không thể tưởng tượng được ! Ông đã kết hợp được trong ông, hai con người có hai thái cực khác nhau.
Sự thể là sau ba năm du học, vào năm 1955 từ Pháp trở về, ngoài bằng phi công quân sự, thiếu uý phi công NXV còn mang theo về nước một bằng kỹ sư hàng không và một bằng cử nhân cộng thêm cao học toán .
Khi mới về nước, đồn trú tại căn cứ không quân Nha Trang, nơi có biển đẹp và những người con gái có làn da ngăm ngăm, săn chắc, xinh đẹp, và quyến rũ, thay vì theo đuổi một bóng hồng nơi miền thuỳ dương cát trắng để có những buổi chiều mơ mộng sau giờ bay đưa người đẹp đi uống nước bên bãi biển như những chàng phi công khác, ngoài giờ công tác và đi bay, theo lời yêu cầu của bộ Quốc Gia Giáo Dục, và với giấy phép đặc biệt của bộ Quốc Phòng, chàng sĩ quan không quân trẻ Nguyễn Xuân Vinh, cũng để mỗi tuần vài giờ tới trường trung học Võ Tánh ở Nha Trang, để truyền đạt kiến thức toán học của ông cho thế hệ sau.
Ông gắn bó với nghề giáo từ đây. Lại một lần nữa ông kết hợp trong ông hai con ngươì hoàn toàn mâu thuẫn nhau: một con người không quân trẻ tuổi, hào hùng và hào hoa, và một con người nhà giáo, mô phạm, nghiêm túc . Với khả năng văn võ của ông, ông đươcï cả Bộ Tổng Tham Mưu Quân Đội Quốc Gia lẫn Bộ Quốc Phòng xử dụng trong nhiều chức vụ mà một sĩ quan cấp úy trung bình không thể đảm đương nổi. Trong vòng 2 năm từ một trung úy phi công ở Phi Đoàn Liên Lạc và Tác chiến ở Nha Trang, ông được chuyển về Phòng Tổng Nghiên cứu và Kế hoạch ở Bộ Tổng Tham Mưu, rồi được Bộ Tham Mưu Không Quân xin về để giữ chức vụ Trưởng Phòng Tư, sau đó lại được Bộ Quốc Phòng cử sang Sứ Quán Việt Nam ở Hoa Thịnh Đốn như là một vị đại úy Phụ Tá Tùy Viên Quân Lực. Chưa đầy một năm sau, vì nhu cầu quân vụ khẩn thiết nhà văn Toàn Phong Nguyễn Xuân Vinh được Bộ Quốc Phòng gọi về để giữ chức vụ Trưởng Phòng Báo Chí Nha Chiến Tranh Tâm Lý. Thật ra trong chúng ta ít ngưòi biết là trong chức vụ này đã có môt thời ông là chủ bút của hai tờ báo Quân Đội và Phụng Sự của Quân Đội Quốc Gia với một ban biên tập có những nhà văn nhà thơ và nhà báo nổi danh đương thời như Thanh Nam, Tô Kiều Ngân, Huy Sơn, Huy Quang, Tường Linh, Nguyễn Ang Ca, …. Nhưng nghiệp bay vẫn trở lại với ông và cuối năm 1957 Thiếu tá Nguyễn Xuân Vinh được bổ nhiệm vào chức vụ Tham Mưu Trưởng Không Quân Việt Nam và năm tiếp theo, khi mới 28 tuổi, Trung tá phi công Nguyễn xuân Vinh, qua những nhiệm vụ liên tiếp, đã chứng tỏ được khả năng tham mưu và chỉ huy để được Tổng Thống VNCH giao cho đảm nhận chức vụ Phụ tá Không quân cho Đại Tướng Tổng Tham Mưu Trưởng Quân Đội Quốc Gia Viêït Nam. Trong cương vị này, với tổ chức buổi đầu của Không quân Việt Nam vẫn còn sơ sài, ông Nguyễn Xuân Vinh là người đầu tiên chịu trách nhiệm hoạch định tất cả các chương trình phát triển để Không Quân thành một quân chủng riêng biệt, có một Bộ Tư Lệnh Không Quân, có khả năng kỹ thuật và hành quân, tạo được sự kính nể của các Không Quân bạn trong vùng Thái Bình Dương.

với cương vị Tư Lệnh KQVNCH
Trong thời điểm này, một bí mật quân sự quốc gia được thực hiện, và nay đã giải mật, đó là chương trình thả “Biệt kích nhẩy Bắc.” Lại chính con người có bề ngoài hiền lành này, với tư cách là tư lệnh quân chủng không quân, là một trong những người đầu tiên tham gia cùng với các vị tư lệnh quân binh chủng và đại đơn vị khác hoạch định kế hoạch. Trong những phi vụ thả “Biệt kích Nhẩy Bắc” đầu tiên, Tư lệnh không quân Nguyễn Xuân Vinh, không những là người tham gia hoạch định kế hoạch mà còn là người tiễn chân các “Kinh Kha” tại ngay phi đạo .

Nhưng tư lệnh không quân Nguyễn Xuân Vinh không từ bỏ được nghề giáo, môi trường duy nhất lúc đó có thể giúp ông sống với toán học. Với giấy phép của Bộ Quốc Phòng vẫn còn hiệu lực, ông xắp xếp công việc để có thể dậy thêm ít giờ tại hai trường trung học Chu Văn An và Petrus Ký về hai môn Hình học Không gian và Thiên Văn học. Trong khoảng thời gian này, con người mê thơ văn từ thuả thiếu thời trong ông lại trỗi dậy. Ông đã từng nhắc lại một câu của toán học gia lừng danh Đức quốc là ông Karl Weierstrass (1815-1897) rằng, “một toán gia, nếu không là một thi sĩ thì không thể nào là một toán gia toàn vẹn được!”. Cho nên, vừa chỉ huy đại đơn vị, vừa nghiên cứu toán học, vừa dậy học, ông vừa làm thơ. Và có lẽ chính ông đã mở đường cho một trào lưu thơ, mà nhiều người đã gọi một cách vui là “Thơ Tình Toán Học .” Tôi xin nhắc lại vài câu mở đầu trong bài “Tình Hư Ảo” cuả Toàn Phong sau đây:
Tình Hư Ảo
Anh tìm em trên vòng tròn lượng giác,
Nét diễm kiều trong tọa độ không gian.
Đôi trái tim theo nhịp độ tuần hoàn,
Còn tất cả chỉ theo chiều hư ảo.
Bao ước mơ , phải chi là nghịch đảo,
Bóng thời gian, qui chiếu xuống giản đồ .
Nghiệm số tìm, giờ chỉ có hư vô,
Đường hội tụ, hay phân kỳ giải tích.
Cũng chính trong thời gian này, cuốn “Đời phi công” ra đời làm nô nức mọi thanh niên thiếu nữ, đang mơ mộng hải hồ hay mơ có ngừơi yêu là một chàng không quân hào hoa cưỡi gió, đè mây. Cuốn tiểu thuyết này đã đoạt giải Văn Chương Toàn Quốc năm 1961. Định mệnh đã làm cho hoạt động của người không quân Nguyễn Xuân Vinh vượt khỏi tầm vóc quốc gia để sau này tên ông được thế giới biết đến. Cho nên , sau khi đã tạo ra được cái khung để lực lượng không quân non trẻ của VNCH dưạ theo đó mà phát triển, tư lệnh Nguyễ Xuân Vinh, có lẽ một phần cũng do bản chất lớn lên trong một gia đình thấm nhuần nho giáo, nên ông đã xuất xử theo phong cách cuả kẻ sĩ đông phương, là “gác kiếm từ quan!” Ông đệ đơn xin từ chức tư lệnh không quân để đi du học. Năm 1962, ông lên đường đi du học nhưng vẫn còn là một quân nhân. Có lần tôi hỏi ông thế không phải ông bị tổng thống Diệm cho bãi chức tư lệnh và đẩy ông đi du học vì vụ hai phi công Quốc và Cử ném bom dinh Độc Lập à? Ông ngạc nhiên, không biết rằng bên ngoài dân chúng người ta tưởng và tin như thế. Như thường lệ, ông nhỏ nhẹ cho biết việc ông nghỉ chức tư lệnh không quân không liên quan gì tới vụ ném bom của hai phi công Quốc, và Cử. Ông đã làm tư lệnh không quân gần 5 năm trong khi ở các nước tân tiến nhiệm kỳ của các tư lệnh quân chủng thường chỉ là 4 năm mà thôi. Ông cho biết tiếp lúc vụ ném bom xảy ra ông đang ở nước ngoài. Và sau khi xẩy ra biến cố này phải 6 tháng sau ông mới lên đường du học. Ông có vẻ tin ở số mạng. Ông cho biết thêm trong đời ông có nhiều may mắn, và thường trong công việc bao giờ cũng được trên thuận dưới hoà. Ông tâm tình cho biết, các cấp chỉ huy trong Không Quân Hoa Kỳ rất nể trọng ông và họ đã đặc biệt dành trong ngân sách viện trợ một học bổng cho ông được đưa theo cả gia đình theo học chương trình tiến sĩ khoa học hàng không và không gian tại University of Colorado . Ở nơi đó họ cũng mời ông tới thuyết giảng hai lần ở trường Võ Bị Không Quân ở Colorado Springs.
Chỉ ba năm sau, vào năm 1965, vị cựu tư lệnh Không Quân VNCH đã được ghi tên vào lịch sử của tiểu bang Colorado như là người đầu tiên được cấp bằng tiến sĩ (Ph.D) về ngành Aerospace Engineering Sciences tại trường Đại học Colorado. Ông được mời ở lại dậy học và xin được bộ Quốc Phòng Việt Nam cho từ dịch và được cấp thẻ thường trú của Hoa Kỳ để nhận chức giảng sư của Đại học Colorado . Năm 1968, Ông được mời tới dậy ở Đại học Michigan và năm 1972 ông được thăng chức giáo sư thực thụ (tenured full professor). Tới khi về hưu năm 1998, ông được phong chức “Giáo sư vĩnh viễn” (Professor emeritus) tại trường đại học này.
Cũng năm 1972 ông dành được thêm bằng tiến sĩ quốc gia toán học tại Đại học Paris . Giáo sư Nguyễn Xuân Vinh đã là thày dậy cho vào khoảng gần hai ngàn kỹ sư hàng không và không gian cho nhiều trường đại học ở Hoa Kỳ và nhiều nước trên thế giới. Học trò của ông nhiều người đã trở thành giáo sư đại học và nhà nghiên cứu xuất sắc. Ông đã xuất bản 3 cuốn sách và gần 100 bài khảo luận về toán học, về chuyển động của các thiên thể và phi thuyền không gian và về quĩ đạo tối ưu. Nhiều bài viết của ông đã được chuyển dịch sang Pháp, Nga và Hoa ngữ. Nhiều công thức ông tìm ra đã được dùng trong những sách giáo khoa ở các nước Pháp, Nga và Nhật Bản mà những tác giả đã căn cứ lên những tài liệu và sách ông viết ở Hoa Kỳ.
Thành quả về nghiên cứu khoa học và giáo dục khoa học không gian tại các trường đại học trên thế giới cuả ông được liệt kê khá nhiều trong những tài liệu để ở những thư viện chuyên khoa. Ông cũng nhận được nhiều giải thưởng trên nhiều lãnh vực, chưa kể trong lãnh vực giáo dục và nghiên cứu khoa học không gian là lãnh vực chuyên môn của ông. Tôi thấy thật là khó viết cho đầy đủ hay nói cho trọn vẹn trong một khuôn khổ hạn hẹp những thành quả của giáo sư Nguyễn Xuân Vinh. Tôi nhớ là nhà thơ và triết gia Võ Thạnh Văn đã có lần nói ông muốn có dịp để nói trong ba giờ liền sự nghiệp của giáo sư Nguyễn Xuân Vinh. Suốt năm qua, có dịp cùng với bác sĩ Phạm Đức Vượng làm việc chung với ông, tôi được biết thêm nhiều điều mà người ngoài không biết.
Giáo sư Toàn Phong Nguyễn xuân Vinh không chỉ là một khoa học gia không gian “đầu tiên” và “hàng đầu” của Việt Nam , mà ông còn có vị trí rất lớn trong ngành không gian thế giới. Điều này ngày xưa ở Việt nam tôi chỉ nghe nói nhưng cũng không hiểu thấu đáo nhất là Việt nam ta hay “nói quá” về những thành tích cuả người mình. Nhưng có lần cùng bác sĩ Vượng đứng với ông trong căn phòng làm việc nhỏ bé tràn đầy sách vở dưới sàn, bít cả lối đi, tôi giật mình rung động trước những tấm plaques và bằng khen ngợi của các cơ quan quốc tế và Hoa Kỳ dành cho những đóng góp cuả ông cho khoa học không gian thế giới. Đặc biệt tôi chú ý tới cái bằng và huy chương của American Institute of Aeronautics and Astronautics (viết tắt là AIAA) là Hiệp Hội của tất cả các kỹ sư và khoa học gia Hoa Kỳ trong ngành Hàng không và Không gian mới khen ngợi các đóng góp cuả ông trong cả 2 lãnh vực vừa trong bầu khí quyển (atmosphere) vừa trong không gian ngoại từng khí quyển (space). Huy chương này, mỗi năm AIAA chỉ tặng cho một khoa học gia không gian duy nhất. Gần ông và được thấy những chồng sách trong phòng làm việc của ông tôi mới được biết ông là người Á châu đầu tiên và là người Việt nam độc nhất được bầu vào Hàn Lâm Viện Hàng không và Không gian Pháp quốc, một Hàn Lâm Viện mà số hội viên hạn chế, đã có những danh nhân như nhà kiến trúc hàng không Marcel Dassault, như cựu thủ tướng Michel Debré, một trong 40 ông viện sĩ bất tử trong Hàn Lâm Viện Pháp . Sau GS Vinh, người Á châu thứ nhì được bầu vào Hàn Lâm Viện này là kỹ sư hàng không Bacharuddin Habibie, cựu tổng thống của Nam Dương. Trong những bảng lưu niệm tặng cho những thuyết trình viên danh dự ở các hội nghị, tôi thấy ông được mời tới nói chuyện ở Hội Nghị Thường Niên của Ủy Ban Điều Hợp Nguyên Tử Lực Hoa Kỳ ở Maryland và ở Hội Nghị Lưỡng Niên Toàn Cầu của Công ty Hoá chất Dupont ở Delaware. Tôi không ngờ là ông cũng nổi tiếng trong hai lãnh vực Nguyên Tử Lực và Hoá Học nên hỏi ông về điều này. Ông lắc đầu trả lời: “Kiến thức về Vật Lý và Hoá Học của tôi chỉ ở mức trung bình như một người thường. Họ không mời tôi đến nói về những môn khoa học chuyên môn mà về một đề tài tôi tự lựa chọn. Như ở Hội Nghị Nguyên Tử Lực tôi nói về đề tài “Exploration of Inner Space” có ý nghĩa là con người đã có những thám hiểm ở ngoài không gian (outer space) thì cũng nên có lúc tìm hiểu về nội tâm (inner space) của chính mình.”
Câu nói trên của ông có thể dùng để biểu hiện con người và thành tích của giáo sư Nguyễn Xuân Vinh. Ông là một kết hợp của những mâu thuẫn; nhưng đó là một sự kết hợp hài hoà khiến ông trở thành một con người tài hoa, đa dạng. Vừa là một quân nhân, vừa là một phi công, vừa là một tư lệnh, vừa là một nhà giáo, vừa là một nhà văn, vừa là một nhà thơ, vừa là một nhà hoạt động quần chúng, nhưng thành quả to lớn nhất trong cuộc đời ông theo tôi nghĩ đã vượt biên giới quốc gia, và vượt thời gian là những đóng góp cuả ông trong ngành hàng không không gian thế giới . Với công trình to lớn đó, mà tôi nghĩ là ông đã thành tựu với ý nguyện góp phần của một người Việt vào sự tiến hoá của nhân loại, ông thực đã mang lại sự hãnh diện chung cho dân tộc.
Nguyễn Tường Tâm, 4/10/2005

Tác phẩm Vui đời toán học ra mắt cộng đồng người Việt tai Orange County lúc 11:00 SÁNG, NGÀY CHỦ NHẬT, NGÀY 13 THÁNG 1 NĂM 2013, tại HỘI TRƯỜNG VĂN LANG, 14861 Moran Street, Westminster, CA 92683.
Trong cuộc sống thường nhật của chúng ta, rất nhiều vật dụng, đồ đạc, phương tiện chúng ta cần dùng, ít nhiều liên quan đến toán, ví dụ như hệ thống định vị toàn cầu (GPS, Global Positioning Systems) dùng trong các xe ô tô, máy computer, Ipod, cell phone,… to lớn hơn có phi cơ, tàu thùy, freeways, cầu cống,… Các thứ này do con người thiết kế dùng toán học tính ra. Do vậy toán học thực sự quan trọng đối với con người. Và con người đam mê, gần gủi với toán học, và gần gủi trong đề tài này, tôi nghĩ đến tác giả sách Vui Đời Toán Học, của GS Nguyễn Xuân Vinh. Tựa đề như vậy nghe có vẻ như tác phẩm này quá chuyên về toán chăng? Thưa rằng theo tôi đúng và không đúng. Đúng đối với những độc giả ít va chạm đến môn toán, ví dụ các trang như trang 53 đến 85 phần Đường trời muôn vạn nẻo, tính Đạn đạo tầm xa của phi đạn khai hỏa đến bài theo ánh tinh cầu, tác giả ôn qua đề tủ Lý Thuyết Phương Sách Tối Ưu (Theory of Optimal Process). Những trang từ 95 đến 118, phần Địa cầu trong không gian có những công thức cơ bản tính toán trong môn Thiên văn học. Có những chương tác giả chỉ đi phớt qua ý niệm toán ứng dụng nhập môn, không đào sâu vào tận gốc rễ của vấn đề như sách giáo khoa hay những bài tham luận chuyên ngành (technical term papers). Phần tác phẩm không đúng là sách toán vì có những trang lại thuần văn chương thi ca, một khía cạnh mà tác giả mê say.

Tưởng cũng nên ghi nhận tác giả là một vị giáo sư toán giảng dạy bậc cấp cao (advanced mathematics), và cũng là một khoa học gia ngành không gian, mà đề tủ của ông là Optimal Trajectories, ông viết sách về Quỹ Đạo Tối Ưu, sách toán hay không gian học của Mỹ, Pháp, Nga, Nhật,… đều có đăng những bài do ông viết. Do vậy tác giả Nguyễn Xuân Vinh là người của thế giới, họ biết ông qua những kiến thức chuyên môn của ông, mà toán học và không gian học là hai yếu tố then chốt tạo nên tên tuổi của tác giả. Nói như vậy không có nghĩa là Vui Đời Toán Học được ươm mầm bởi những lý thuyết toán học cao siêu của những Joseph Lagrange, Laplace, Euler, Fourier, Boole, Cauchy, Leibniz, Isaac Newton, Jacob Bernoulli, Johann Bernoulli, Bourbaki, Neumann, Niels Abel, Plato, Blaise Pascal, Pythagore, René Descartes,… Nhưng theo ý tôi như trên đã đề cập tác giả chỉ dùng những khía cạnh toán học để chia sẻ sang những đề mục khác như: cuộc sống, văn chương, xã hội, kỷ niệm khi dạy học,… ví dụ như chương về Đường Trời Muôn Vạn Nẻo (trang 29 qua các bài viết như Tâm sự qua một bài thơ, Mấy nhịp cầu treo, Lời tiên tri của Voltaire, Theo ánh tinh cầu,…), Nguyễn Du với dòng thời gian (trang 285 trích thơ Nguyễn Du đầy ắp, đây là chương hoàn toàn mang nét Toàn Phong, bút hiệu viết văn, chương này tác giả bình luận về thơ của thi hào Nguyễn Du qua cái nhìn của mình trong cuộc sống, rồi sau cụ Nguyễn Du lại đến Nhớ về Thăng Long (trang 313 tác giả dùng thơ của nữ sĩ Bà Huyện Thanh Quan làm đề tài diễn giải), Cây Tháp ở Hà Nội, Nhớ về Hà Nội,…, phần kế là Tình toán học (chương sách kể sự liên hệ giữa tác giả và sự đam mê toán học, trang 365 như Thuở ban đầu, Chuyên khoa toán học, Chương trình tiến sĩ,…), Trở về trường xưa (trang 405),…

Hàng Không-Không Gian Quốc Gia Hoa Kỳ (NASA)
Tham khảo:
http://www.dunglac.org/index.php?m=module2&v=detailarticle&id=279&ia=5992
Các chủ đề hay các bài viết của Toàn Phong Nguyễn Xuân Vinh mà tôi vốn thích là Theo Ánh Tinh Cầu, Mộng Viễn Phương, và Tình Toán Học. Toàn Phong viết về quê hương trong hoài niệm thuở nhỏ như trong bài “Một Thuở Học Trò” đề cập về buổi khai trường lần đi học đầu tiên, nghe như thư tác của nhà văn Edmondo de Amicis, hoặc là của Thanh Tịnh của “Hằng năm cứ vào cuối thu, lá ngoài đường rụng nhiều và trên không có những đám mây bàng bạc, lòng tôi lại nao nức những kỷ niệm hoang mang của buổi tựu trường….“
Tôi mê thuở đi học từ Việt Nam sang Huê Kỳ, những buổi học xưa sẽ lý tưởng khi mà rảo bước trong campus mùa thu lá maple vàng úa rụng nhiều, chạnh lòng đến văn chương của Thanh Tịnh, của Amicis hay của Toàn Phong. Theo Ánh Tinh Cầu cho tôi nghĩ ngợi lan man về văn học mà khoa học viễn tưởng của những chuyến du hành vào vũ trụ tiên khởi của Jules Verne, hay Hoàng Tử Bé (danh tác của Pháp là Le Petit Prince) của nhà văn kiêm phi công gốc Pháp Antoine de Saint-Exupéry. Với Mộng Viễn Phương, nhà văn Toàn Phong hoài niệm về giấc mộng tung hoành xé không trung qua tổ quốc không gian hay tác phẩm bestseller Đời Phi Công, mà tôi đọc nhiều lần nó có những địa danh như Marrakech, hoặc école de pilotage à Aix-en-Provence,…

Nhà văn kiêm nhà giáo môn toán Nguyễn Xuân Vinh yêu thích thi ca, Vui Đời Toán Học ghi nhận trong nhiều trang sách. Trong tương quan đó nữ toán học gia gốc Nga Sophia Kovalevskaya của thế kỷ 19 cho là: Bạn không thể là một nhà toán học mà không có tâm hồn của một nhà thơ (Il est impossible d’être un mathématicien sans avoir poète dans l’âme). Còn nhà toán học người Đức nổi danh trong môn toán Calculus, Karl Weierstrass (cuối thế kỷ 19) cho nhận định: Một nhà toán học không mang một nét gì đó của một nhà thơ thì chả bao giờ là một nhà toán học trọn vẹn được (Un mathématicien qui n’est pas aussi quelque peu poète ne sera jamais un mathématicien complet). Tôi thầm nghĩ chả nhẽ hai cụ Sophia Kovalevskaya và Karl Weierstrass đã cho hai câu nói đúng y bong để giới thiệu về nhà văn kiêm giáo sư có hai đam mê trong tâm hồn, toán học và văn học, GS. Toàn Phong Nguyễn Xuân Vinh.
Như phần mở đầu đề cập mối liên hệ giữa toán học và cuộc sống, tôi xin đúc kết bài giới thiệu qua ý tưởng của toán học gia John von Neumann (Mỹ gốc Hung, thế kỷ 20), nôm na cho ý là: Nếu mọi người không tin rằng toán học là đơn giản, cũng bởi vì họ không nhận chân ra là cuộc sống phức tạp như thế nào (Si les gens ne croient pas que les mathématiques sont simples, c’est uniquement parce qu’ils ne réalisent pas combien la vie est compliquée.)
Thật vậy nhờ môn học toán được phổ thông hóa giảng dạy ở trường học ở các cấp, và rồi nó được đem vào ứng dụng trong đời sống, các phát minh khoa học kỹ thuật tân tiến, cuộc sống con người tiện nghi hơn, thoải mái hơn, GS. Nguyễn Xuân Vinh cho nhiều cảm nghĩ trong tác phẩm mới của ông, tôi đơn cử một bài viết khác như dưới đây.
Theo website Nguồn Cội đăng bài giới thiệu về sách Vui Đời Toán Học, qua bài viết Vẻ Tuyệt Mỹ của Hình Tròn của GS. Nguyễn Xuân Vinh. Xin mời đọc.
VUI ĐỜI TOÁN HỌC của Giáo Sư Tiến sĩ Nguyễn Xuân Vinh, dựa theo như lời của GS Vinh thì tập truyền này dài khoảng 350 trang, bao gồm nhiều chương xoay quanh TOÁN HỌC, cũng như Văn Hóa, Tình Yêu, kỷ Niệm trong Toán Học như: Địa Cầu Trong Không Gian; Galois, Thiên Tài và Bất Hạnh; Nguyễn Du Với Dòng Thời Gian; Nhớ Về Thăng Long; Con Ong Giỏi Toán; Một Bài Toán Thần Sầu; Một Thuở Học Trò; Tình Toán Học; Mười Hai Bến Nước; Trải Hương Theo Gió; Trở Về Trường Xưa; The 3 D’s of Nguyen Xuan Vinh …vân vân…và trong mỗi chương lại có thêm nhiều tiểu đề nhỏ nữa .
Trích theo lời giới thiệu của Nguồn Cội, đăng tiểu đề Vẻ Tuyệt Mỹ của Hình Tròn, tiểu đề này gồm có 5 tiểu đề nhỏ như sau:
1) Những tiên đề của Euclid và hình tam giác của phương Đông
2) Hình lục lăng của phương Tây và những cây cầu của thành phố Konigsberg
3) Hình ngũ giác của phương Nam và điện Parthenon của Hy Lạp
4) Hình vuông của phương Bắc và định lý của Pythagoras
5) Hình tròn và tính chất siêu việt của số Pi

Trong câu chuyện này, tôi sẽ nói về những vẻ đẹp tuyệt vời của hình tròn. Từ khi loài người biết suy nghĩ, ban đêm nhìn thấy sao hiện ra rồi lấp ló có ánh trăng. Chờ đợi từng ngày, cho đến ngày rằm, lúc trăng tròn, hiện ra suốt đêm từ hoàng hôn cho đến rạng đông, hình thể mặt trăng lúc đó được coi là tuyệt mỹ. Ðứng bên một mặt hồ phẳng lặng, ta có thể bỗng nhiên nghe tiếng cá đớp và nhìn ra sẽ thấy những ngấn nước loang dần dần theo những vòng tròn đồng tâm. Hay có thể một buổi sáng, sau cơn mưa nhìn về phía Tây, con người nhìn thấy một cầu vồng mầu sắc vẽ một vành cung lớn trên nền trời. Ðó là những hình tròn thiên nhiên con người nhìn thấy từ thời thạch động. Khi con người nghĩ ra được bánh xe tròn là lúc đó phương tiện chuyển vận đã được một bước nhẩy vọt không khác gì khi chế ra được chiếc thuyền để đi trên mặt nước hay khi dùng được máy hơi nước để chuyển vận những toa tầu trên đường sắt. Thi nhân đã không tiếc lời ca tụng mặt trăng, cho đến nỗi khi tả sắc đẹp của mỹ nhân cũng nghĩ rằng mặt người nếu tròn như mặt trăng đêm rằm là mặt đẹp như đoạn Nguyễn Du tả Thúy Vân:
“Vân xem trang trọng khác vời
Khuôn trăng đầy đặn, nét ngài nở nang”
Nhưng bạn đọc có thể hỏi tại sao lại chọn hình tròn và cho hình này là hình đặc sắc nhất. Trước đây ta đã có dịp gặp những hình Cycloid, đã được gọi là nàng tiên đẹp Helen của thành Troy, ta đã thấy hình Catenary tức là hình nếp áo treo của tiên nữ, ngoài ra còn biết bao nhiêu hình khác các nhà toán học đã tìm ra trải qua ba nghìn năm nghiên cứu. Vì vậy để hiểu được vị trí của hình tròn trong toán học, chúng ta trước hết hãy duyệt qua một số hình đặc sắc khác trước khi đi đến kết luận hình nào là hình đẹp tuyệt vời.
Chúng ta chắc nhiều người đã đọc những chuyện võ hiệp và đã được biết có một thời trong võ lâm có năm bậc tài năng tới mức thượng thừa. Năm vị lãnh tụ võ lâm ấy là Hoàng Dược Sư, Âu Dương Phong, Ðoàn Nam Ðế, Hồng Thất Công và Vương Trùng Dương mỗi vị trấn một phương, uy thế ngất trời. Một lần họ họp với nhau suốt bẩy ngày và bẩy đêm trên đỉnh núi Hoa Sơn để bàn luận võ công, tuy không thực sự quần thảo nhưng dùng lý thuyết và biểu diễn tranh tài cao thấp. Chung cuộc họ đi đến kết luận là người nào cũng đã đến tuyệt đỉnh môn phái võ của mình. Âu Dương Phong có môn Hàm Mô Công thật là ác độc, Hoàng Dược Sư là một nhà thông thái võ công huyền ảo, kỳ bí, có phần chính, có phần tà, vị Ðế Vương miền Vân Nam họ Ðoàn được thừa hưởng môn võ Nhất Dương Chỉ truyền đời, chỉ dùng ngón tay mà tạo ra những đường kiếm linh hoạt, ảo diệu. Ngoài ra Hồng Thất Công là vị bang chủ Cái bang, tính tình hào hiệp, trọng nghĩa khinh tài, môn Giáng Long có mười tám thế đánh bằng tay sức mạnh ví như có thể di sơn, đảo hải, lại thêm môn võ đánh gậy trúc gọi nôm na là Ðả Cẩu Bổng Pháp tuy nhẹ nhàng nhưng lại huyền diệu lợi hại khôn lường. Tuy không tôn một ai làm minh chủ của võ lâm nhưng các vị lãnh tụ đều phải nhận là giáo chủ Vương Trùng Dương, xưa nay vẫn ẩn cư ở núi Chung Nam, võ nghệ, kiến thức tuyệt luân, tính tình lại từ hòa nhân ái đáng giữ ngôi vị ở trung ương. Từ đó truyền bá ra Võ Lâm theo phương vị là Ðông Tà, Tây Ðộc, Nam Ðế, Bắc Cái, Trung Thần Thông, ý nói là Hoàng Dược Sư giữ ngôi vị chúa đảo ngoài Ðông Hải, trong khi đó Âu Dương Phong hùng cứ miền Tây Nguyên, Ðoàn Vương Gia là thủ lãnh suốt miền Nam và Hồng bang chủ trấn ngự toàn phía Bắc. Ở trung ương thì ngôi vị phải nhường cho con người võ nghệ siêu phàm là Vương Trùng Dương chân nhân.
Tôi nghĩ rằng trong hình học, lựa chọn ra một hình có tính chất tuyệt luân huyền diệu cũng khó như cuộc luận kiếm trên đỉnh Hoa Sơn. Vì vậy tôi tưởng tượng ra đây một trại Hè tôi và một số bạn trẻ đã qua mấy ngày đêm thảo luận về những nét hay đẹp của một số hình trong toán học và giờ đây duyệt lại xem hình nào đáng giữ ngôi vị trung ương. Ðể buổi hội thảo có trật tự, ta tạm chia nhiệm vụ là đã có bốn nhóm trại sinh, mỗi nhóm đã nghiên cứu và chọn ra được một hình như là cao thủ võ lâm để dự cuộc tuyển chọn và hiện nay 4 nhóm này đã ngồi chung quanh theo bốn phương vị Ðông, Tây, Nam và Bắc. Số người còn lại, hoặc chưa có ý kiến, hoặc chưa đưa ra hình dự cuộc vì còn muốn giữ bí mật nay ngồi ở phần giữa của hội trường.
MỘT VÀI TÁC PHẨM VIẾT BẰNG TIẾNG ANH, HÌNH ẢNH DO GS TRẦN HUY BÍCH CUNG CẤP



Những Tiên Ðề của Euclid và Hình
Tam Giác của Phương Ðông
Ngồi ở Ðông vị là một nhóm trông có vẻ hăng hái hơn cả vì muốn được xuất quân trước nhất. Một bạn đại diện đứng lên và đưa đề nghị thật giản dị:
“Hình đẹp nhất phải là hình tam giác được tạo ra bởi ba điểm A, B và C không thẳng hàng nối với nhau bằng những đoạn thẳng và trong tất cả các hình tam giác vẽ được trong thế gian, hình tuyệt mỹ là hình tam giác có ba cạnh đều nhau.”
đó có nhiều bạn trong nhóm Ðông mỗi người đứng lên nói một câu biện minh cho sự chọn lựa của nhóm này. Tôi ghi lại đây những ý chính:
Nếu chỉ có hai điểm thì không vẽ ra được một hình. Phải có ít nhất là ba điểm. Vậy tam giác là hình giản dị nhất, thiên nhiên nhất và dĩ nhiên là đẹp nhất.
Làm một cái bàn chỉ có hai chân thì không thành cái bàn. Phải cần có ba chân, thành ra ba điểm đặt, và ba điểm là vững vàng nhất. Dùng bốn điểm có thể thành khập khễnh.
Tam giác ba cạnh đều là tam giác cân xứng nhất vì có ba cạnh bằng nhau và ba góc đỉnh cũng bằng nhau. Ngoài ra, trên một mặt phẳng, muốn ghép những hình đều cạnh mà không để chừa ra khoảng trống, như lát sàn bằng gạch hoa, thì chỉ có thể dùng hình tam giác đều, hình vuông và hình lục lăng đều như Hình 1. Trong ba kiểu hình này thì tam giác đều có ít cạnh nhất, như vậy giản tiện mà lại thỏa mãn điều kiện lát gạch.
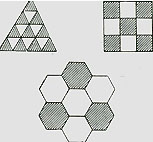
Ðến đây với tính cách là người điều khiển buổi hội thảo đầy hứng thú này, tôi muốn có ít lời nhận xét vì lời đề nghị của nhóm Ðông có liên quan đến những tiên đề của hình học.
Trước hết tiên đề là gì? Ở thế kỷ này và trong tương lai, ở những thế kỷ tiếp nối, hay cả ở những hành tinh khác trong vũ trụ, nếu có những người thông minh xây dựng được môn toán học riêng của họ, thì môn nào cũng phải dựa vào luận lý. Lấy thí dụ trong hình học là môn toán học ta tìm ra được những tính chất gọi là a, b và c mà những tính chất này được suy đoán một cách minh bạch, không ai chỉ trích nổi, từ những tính chất mà ta gọi là d, e và f thì những tính chất sau này được coi là những tính chất khởi thủy để dùng luận lý mà xây dựng ra môn hình học. Nay ta lại xét đến những tính chất d, e và f khi những tính chất này không phải dùng những lý luận loanh quanh mà suy ra lẫn nhau mà lại được suy ra một cách rất rõ ràng từ những tính chất khác mà ta gọi là g và h, thì những tính chất sau này mới gọi là tính chất khởi thủy vì tự nhóm này mà ta đã dùng luận lý để suy ra những tính chất d, e và f, và tiếp theo đó suy ra những tính chất a, b và c. Mỗi lần suy luận một cách minh bạch, dựa vào những gì đã được công nhận để tìm ra những tính chất tiếp theo ta nói là đã chứng minh được một định lý. Nếu ta đi ngược lại về nguồn thì sẽ tới được những tính chất nguyên thủy không có thể dựa lên những tính chất nào khác nữa để chứng minh những tính chất nguyên thủy này mà ta gọi là tiên đề.
Vậy tiên đề là những khái niệm gì ta phải công nhận, không cách gì chứng minh được, và căn cứ vào đó ta xây dựng nên cả môn toán học.
Người đầu tiên đã đặt thành hệ thống môn hình học dựa vào những tiên đề là nhà giáo Euclid, viết sách và mở trường dậy vào khoảng những năm 330-275 trước Công nguyên ở Alexandria bên Ai Cập, tuy ông lại là người Hy Lạp. Ông đúng là nhà soạn sách thành công nhất tự cổ xưa tới nay vì hơn hai ngàn năm qua, môn hình học đã được khai triển dựa vào những tiên đề và những căn bản viết trong bộ sách 13 cuốn của ông được đặt tên là “Các Cơ Sở”
Ðúng ra thì Euclid viết 10 tiên đề, áp dụng chung cho toán học, nhưng riêng cho môn hình học, sau nhiều thế kỷ tranh luận, sửa đổi, người ta lấy 5 tiên đề, mà 4 tiên đề đầu được lập theo từ chương mới trong những sách giáo khoa hình học như sau:
1. Qua hai điểm có thể xác định được một đường thẳng và chỉ một mà thôi.
2. Qua ba điểm không thẳng hàng có thể xác định được một mặt phẳng và chỉ một mà thôi.
3. Nếu đường thẳng có hai điểm nằm trong mặt phẳng thì đường thẳng đó hoàn toàn nằm trong mặt phẳng này.
4. Nếu hai mặt phẳng có một điểm chung thì chúng sẽ có thêm một điểm chung thứ hai nữa.
5. Tiên đề thứ năm là tiên đề được tranh luận nhiều nhất, tôi sẽ nói ở phần cuối của mục này. Tới đây ta cần nhận định rằng, theo định nghĩa thì tiên đề là những mệnh đề toán học phải công nhận vì không còn mệnh đề nào khác để chứng minh được. Vì vậy ta phí mất công sức để chẳng hạn dùng tiên đề 1, 2 và 3 để chứng minh tiên đề 4 vì nếu chứng minh được thì mệnh đề 4 không còn được gọi là tiên đề nữa. Phần khác ta sẽ thấy là không thể nào thêm được một tiên đề nào khác nữa Chẳng hạn, ta tự nghĩ rằng mình là một thiên tài toán học mà đặt thêm tiên đề thứ sáu.
6. Hai mặt phẳng cắt nhau theo một đường thẳng.
Ðọc lên nghe có vẻ ngon lành như khi vào một tiệm ăn cầm thực đơn mở đôi ra thì sẽ như hiển hiện ra tiên đề thư sáu. Vả chăng, nếu ta đọc lại những tiên đề 1, 2 và 3 thì thấy cũng như là thể hiện những gì hữu hình thường nhật, chẳng hạn một sợi chỉ căng giữa hai điểm (tiên đề 1), một tấm bìa cứng đặt trên ba mũi nhọn (tiên đề 2) và đặt cái thước trên một mặt bàn (tiên đề 3). Vậy tại sao mệnh đề 6 không được gọi là tiên đề nhỉ ?
Ta phải lý luận như sau. Nếu hai mặt phẳng cắt nhau thì chúng phải có một điểm chung và theo tiên đề 4 chúng sẽ có thêm một điểm chung thứ hai nữa. Theo tiên đề 1, ta thấy chỉ có một đường thẳng qua hai điểm này và, theo tiên đề 3 đường thẳng nằm trong mỗi mặt phẳng. Vậy là ta đã dùng tiên đề 1, 3 và 4 để chứng minh mệnh đề 6, và mệnh đề này là một định lý chứ không được gọi là một tiên đề.
Một nhận xét khác nữa là ta đã hình dung ra những điểm, đường thẳng hay mặt phẳng theo định nghĩa hình thể được lý tưởng hóa. Chính vị tổ sư Euclid cũng nhầm lẫn về vấn đề này. Ông tưởng tượng điểm là cái gì không thể thu nhỏ được nữa cũng như một đường là chỉ có chiều dài chứ không có chiều rộng, một mặt thì chỉ có chiều dài, chiều rộng chứ không có bề dầy. Hay đôi khi dùng những cuốn sách nhập môn về Hình Học, để khỏi lúng túng, khi đọc tiên đề 1, học sinh hỏi vặn lại là đường thẳng là gì, hay khi đọc tiên đề 2 có người thắc mắc muốn được biết định nghĩa về mặt phẳng, một nhà giáo khi chỉ có trình độ trung cấp về toán học có thể trả lời là nhìn một sợi chỉ căng là có ý niệm về đường thẳng, hay nhìn một mặt hồ không gợn sóng là có thể hình dung ra được một mặt phẳng. Sự thực ra thì ta có thể công nhận các tiên đề như đã nêu ở trên và không cần phải có định nghĩa về điểm, đường thẳng và mặt phẳng. Thật vậy, nếu bạn đọc có cách nào để quên được những ý niệm hình thể về đường thẳng và mặt phẳng hay tạm cho là đường thẳng có hình hơi cong cong, và mặt phẳng hơi vềnh vồng thì những tiên đề kể trên vẫn đúng như thường vì ta đã mặc nhiên công nhận những tiên đề này. Nếu vì lấy đường thẳng cong cong mà không thích hợp với tiên đề 1 chẳng hạn thì tức là ta đã dùng ý niệm “đường thẳng là cái gì rất thẳng” để chứng minh tiên đề 1 là đúng. Như thế mệnh đề 1 đâu đáng được gọi là tiên đề. Phần khác bạn đọc có thể coi lại đoạn chứng minh mệnh đề 6 khi dùng những tiên đề 1, 3 và 4 sẽ thấy là trong lý luận này chúng ta có dùng ý niệm “đường thẳng là cái gì rất thẳng” và “mặt phẳng là cái gì rất phẳng” để làm hậu thuẫn đâu!
Nay trở lại phát biểu của nhóm Ðông thì ta thấy hình tam giác nằm trong một mặt phẳng và ba cạnh của hình hoàn toàn nằm trong mặt phẳng này. Nhóm Ðông được dành nửa giờ để trình bầy những tính chất đặc biệt của hình tam giác. Dĩ nhiên là có nói nửa ngày trời cũng không hết. Vì vậy các bạn đã nhấn mạnh tính chất hội tụ như sau.
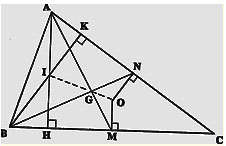
Dựa theo Hình 2: Ba đường trung tuyến vẽ từ 3 đỉnh A, B và C như là đường AM, vẽ từ đỉnh A đến trung điểm M của cạnh đối diện BC, ba đường này gặp nhau ở điểm G là trọng tâm của tam giác và ở 2/3 các trung tuyến kể từ đỉnh.
– Ba đường trung trực tức là những đường thẳng góc với các cạnh như BC vẽ từ trung điểm M, ba đường này cũng gặp nhau ở điểm O là một điểm cách đều ba đỉnh A, B và C. Như vậy, O là tâm điểm cuả vòng tròn ngoại tiếp với tam giác ABC.
– Ba đường cao là là những đường như AH vẽ từ đỉnh A thẳng góc với cạnh đối diện BC, ba đường này cũng gặp nhau ở một điểm I gọi là trực tâm của tam giác.
– Ðặc biệt ba điểm O, G và I lại thẳng hàng với nhau và điểm G ở 2/3 đoạn IO kể từ điểm I. Ðường thẳng này gọi là đường thẳng của Euler.
Nhóm Ðông có vẻ thích thú về những tính chất hội tụ của những đường đặc biệt vẽ trên hình tam giác và các bạn trẻ cho rằng những tính chất này không có ở các hình khác. Một thành viên của nhóm Ðông còn thêm tính chất rằng:
– Nếu vẽ những đường phân giác nghĩa là những đường chia những góc A, B và C, mỗi góc làm hai phần đều nhau thì ba đường này cũng gặp nhau tại một điểm J và điểm này lại đặc biệt ở một vị trí cách đều ba cạnh BC, CA và AB. Như vậy J là tâm điểm của vòng tròn nội tiếp với tam giác ABC.
Sau phần trình bầy của nhóm Ðông tới phần đặt câu hỏi. Câu khó trả lời nhất là:
“Tại sao lại chọn hình tam giác có ba cạnh đều? Ngoài tính chất cốt dùng để lót gạch hoa không có khoảng trống như trên Hình 1, hình tam giác có ba cạnh đều còn có gì đặc biệt? Vả chăng muốn lát kín thì cần gì phải chọn hình có cạnh đều. Chẳng hạn trên Hình 1, thay vì chọn hình vuông, dùng hình chữ nhật có sao đâu ? Những viên gạch xây tường có hình chữ nhật cũng vẫn xếp kín được như thường. Vậy ta cũng vẫn có thể thay hình tam giác ba cạnh đều bằng những hình tam giác cân, chỉ có hai cạnh bằng nhau vẫn xếp kín được như thường chứ ?”
Nghe câu hỏi hóc búa này, thay vì lúng túng, tất cả các bạn trong nhóm Ðông lại vỗ tay reo mừng. Lúc đó họ mới đưa ra môn võ bí hiểm bằng cách trưng ra những Hình 3 và Hình 4. Theo nhóm này thì Hình 3 biểu diễn một định lý tìm ra bởi Hoàng Ðế Napoléon Bonaparte (1769-1821).
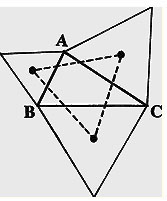
Theo Hình 3: lấy một hình tam giác ABC bất kỳ nào và sau đó, trên những cạnh, kiến trúc ba hình tam giác đều. Trên mỗi tam giác đều, vẽ những điểm gặp nhau của những đường trung trực như điểm O đã cắt nghĩa trên hình 2. Ba tâm điểm này là ba đỉnh của một tam giác ba cạnh đều. Tính chất đặc biệt của định lý này là bất kỳ hình tam giác ABC nào cũng tạo được ra một hình tam giác ba cạnh đều. Ðịnh lý này đã làm cho nhóm ngồi phía Tây là nhóm sắp sửa ra thuyết trình có vẻ nao núng. Tuy vậy, họ cũng có lời phê bình là: “Ðịnh lý của Napoléon phải dùng đến ba hình tam giác đều để kiến trúc ra hình tam giác đều thứ tư. Vậy có gì là bất kỳ đâu ?” Câu hỏi này đi vào bẫy sập của nhóm Ðông vì họ trả lời rằng: “Hãy thử coi Hình 4 sẽ thấy hình tam giác nào cũng đưa đến hình tam giác đều, hay nói văn vẻ hơn, đường nào cũng dẫn đến kinh thành La Mã.
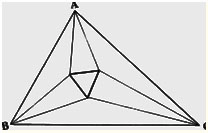
vậy theo Hình 4: bạn thử vẽ một tam giác bất kỳ nghĩa là không có cạnh nào bằng cạnh nào, và như thế cũng có nghĩa là không có góc nào bằng góc nào. Sau đó ở mỗi góc vẽ hai nửa đường thẳng để chia góc làm ba phần đều nhau. Những đường thẳng này cắt nhau tại những điểm là đỉnh của những hình tam giác có ba cạnh đều. Hình vẽ nét đậm trên Hình 4 là một trong những hình tam giác đều được tạo ra.
Sau phần trình bày rất ngoạn mục này, nhóm Ðông đã nhận được một tràng pháo tay cổ võ rất nồng nhiệt. Trước khi giới thiệu phần trình bày của nhóm Tây, chắc cũng không kém phần hào hứng, tôi có chút nhận xét sau đây:
Trở lại lời phát biểu là dùng một cái bàn ba chân là vững vàng nhất, ta thấy là nhóm Ðông đã đi vào phạm vi Cơ học, hay đúng hơn là phần Tĩnh học của Toán áp dụng này. Một cái bàn hay một cái ghế đẩu có ba chân chỉ có thể đứng vững ở vị thế tĩnh khi trọng lực của cố thể này đi qua tam giác hợp thành bởi những điểm đặt. Bạn đọc thử hình dung một mặt bàn đá, nghĩa là khá nặng, có ba chân song song và khá dài. Sau đó, cắt ngắn một chân bàn chút ít sẽ nhận thấy ngay rằng tuy vẫn có ba điểm đặt vững chãi nhưng đường trọng lực, phát xuất tự trọng tâm ở khá cao sẽ đi ra ngoài tam giác đế của chân bàn và chiếc bàn chắc chắn sẽ bị lật nghiêng.
Tiên đề thứ năm của Euclid là: Từ một điểm A ở ngoài đường thẳng b bao giờ ta cũng kéo được một và chỉ một đường thẳng a song song với b. Như đã nói ở trên, trong tập “Các Cơ Sở”, Euclid mở đầu bằng cách phát biểu 10 tiên đề mà trong môn Hình Học dùng 5 tiên đề viết lại theo lối mới như trên. Trải qua hơn hai ngàn năm, nhiều nhà toán học, có những vị là những thiên tài, cho rằng tiên đề 5 chỉ là một định lý hình học có thể suy ra được bằng cách dựa trên các tiên đề khác.
Sau nhiều lần thất bại, phải tới thế kỷ thứ 19, ba nhà toán học lỗi lạc là Carl Friedrich Gauss (1777-1855) người Ðức, Nicolai Ivanovitsch Lobatschewsky (1793-1856) người Nga và Johann Bolyai (1802-1860) người Hung, mới sáng suốt nhận chân rằng tiên đề thứ năm này quả thật là một tiên đề, không chứng minh được vì không suy ra được từ những tiên đề khác. Vị thủy tổ Euclid giữ toàn vẹn chiếc ngai Hình Học, được gọi là Hình Học Euclid. Nhưng mặt khác, các nhà toán học nói trên nghĩ rằng nếu thay thế tiên đề 5 bằng một tiên đề thật trái ngược mà dùng suy luận để đi đến một nghịch lý thì tức là đã chứng minh được tiên đề này, đó là điều đã không ai làm được. Vậy thì có thể dùng một tiên đề khác thay thế cho tiên đề 5 để xây dựng nên một môn hình học mới tức là Hình Học Phi Euclid. Lobatschewsky và Bolyai dựng nên môn hình học mới bằng cách thay tiên đề 5 bằng tiên đề
LB. Từ một điểm A, ở ngoài đường thẳng b, có thể kéo nhiều đường song song với b.
Dùng tiên đề này có thể làm thành một môn hình học trong đó không có gì nghịch lý cả và môn này được gọi là Hình Học Hy-pe-bol. Một môn hình học thứ ba nữa có thể được dựng ra bằng cách dùng một tiên đề trái ngược với tiên đề 5, do nhà toán học Bernhard Riemann (1826-1866) phát biểu là:
R. Từ một điểm A ngoài đường thẳng b không thể kéo đường thẳng nào song song với b.
Môn hình học phi Euclid này được gọi là Hình Học Ellip.
Một nhận xét sau cùng nữa là nhóm Ðông không thể nào chỉ dùng thước kẻ thẳng và com-pa để vẽ nên Hình 4 được. Ðó là vì trong Hình Học có ba bài toán đố không thể nào dùng thước kẻ thẳng và com-pa để tìm lời giải được là các bài sau đây:
1. Chia một góc phẳng bất kỳ làm ba góc bằng nhau.
2. Kiến tạo một hình lập phương có thể tích gấp hai lần thể tích một hình lập phương cho sẵn.
3. Vẽ một hình vuông có diện tích bằng một hình tròn cho sẵn.
Đó là những lời trích từ Vui Đời Toán Học của GS Nguyễn Xuân Vinh.
Việt Hải sưu tầm và nghiên cứu
California 2013

No comments:
Post a Comment